- An array having more than two subscripts is known as multi-dimensional array.
- It can be represented as a series of two-dimension arrays.
Declaration of Multi-Dimension Array:
- We can declare Multi-dimension array using the following syntax:
<data-type> arr-var-name [d1][d2] [d3]…[dn] ;- Here, d1 to dn specifies dimension number.
- The following example declares a three- dimensional integer array of 2 matrices each with 2 rows and 2 columns (2x2x2).
int matrix[2][2][2];- Here, first dimension defines total number of matrix, seconds and third dimension specifies number of rows and columns respectively.
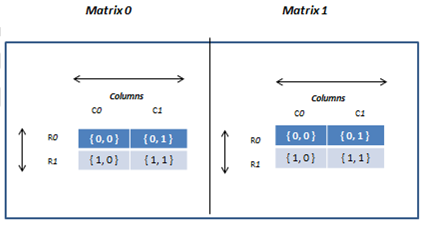
- Memory representation of array matrix can be given as follow:
- Here intersection of rows and columns creates a cell and each cell location can be identified by using its row index and column index similar to two dimension array but since it is three dimension array, it contains additional third dimension that specifies number of matrix so we have to use all three subscript while accessing third dimension array elements.
- For example, for first matrix( 0th matrix) the location of the first element will be 0th row and 0th column ({0, 0, 0}), for second element 0th row and 1st column ( {0, 0, 1 } ), 1st row and 0th column for thirst element ( {1, 1, 0 } ) and 1st row and 1st column for fourth element ( {1, 1, 1 } ).
Initialization of Multi-Dimension Array:
- Similar to two-dimensional array, multi-dimension array can also be initialized either statically or dynamically.
Static initialization:
- We can initialize the above matrix array variable using row and column index either individually or in a group by specifying all the three subscripts as follow:
matrix[0][0][0] = 65;
matrix[0][0][1] = 78;
matrix[0][0][2] = 85;
matrix[0][1][1] = 55;
...- We can combine array declaration and initialization into a single statement as follow:
int x [2][2][2] = { { { 65, 78 } ,
{ 85, 55 }
} ,
{ { 75, 72 } ,
{ 58, 60 }
}
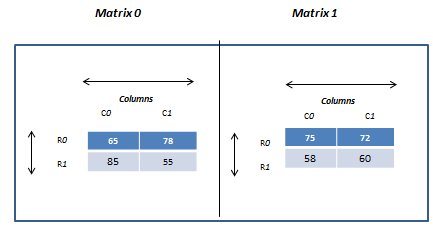
} ;- The above statement will declare array called x of integer types with 2 matrix each with the size of 2 rows and 2 columns.
- Notice that each matrix and row elements are represented in its own set of curly brackets and they are separated by comma.
- It will assign first value (i.e.65) to 0th row and 0th column of first matrix, second value (i.e. 78) to 0th row and 1st column of first matrix and so on.
- Memory representation of array x can be given as follow:
Accessing Multi-Dimension Array Elements:
- We can access each array elements by using all three subscripts i.e. matrix index, row index and column index within square brackets along with array variable name.
- For example, to access the first element of the array x, you can use x [0][0][0], for second element x [0][0][1], and so on.
- The following example performs total of array elements of x by accessing them using their indices.
total = x [0][0][0] + x [0][0][1] + x [0][1][0] + x[0][1][1] ;
Dynamic initialization:
- We can also initialize array at run time. It is referred to as dynamically initialization.
- The following example uses for loop to initialize x array from user at run time.
- Recall that for initialization of two-dimension array we used two loop as it contained two dimensions-row and column.
- Since our array X contains three dimensions: matrix, rows and columns we need three loops to access array elements: the main for loop to keep track of matrix, outer for loop that keeps track of rows and inner for loop that keeps track of column inside the current row.
- The row loop will be executed as per the row size and column loop for the number of columns times as follow:
for ( m=0 ; m < 2 ; m++ ) // iterates over matrix
{
for ( i=0 ; i < 2 ; i++ ) // iterates over rows
{
for ( j=0 ; j < 2 ; j++ ) // columns in current row
{
printf(“\n Enter x[%d][%d][%d]:”, m,i,j ) ;
scanf( “ %d “ , &x [m][i][j] ) ;
}
}
}
- The above for loop is executed for eight times which is the size of our array x and reads eight value from the user and each time counter variable gets incremented and based on its value it is assigned in array x i.e. first value will be stored to x[0][0][0] (as initially m & i is 0 & j is also 0), second value will be stored to x [0][0][1] (as m & i = 0 and j=1) and so on.
- In the case of a three-dimensional array, the following formula is used to compute the number of bytes of memory require storing it:
bytes = size of matrix X size of row X size of column X sizeof(base type)
- For example, bytes required for the given integer array x with size of 2 matrix each with 3 rows and 5 columns will be computed as follow:
int x[2][3][5] ;
total bytes = 2 (size of matrix) X 3 (sizeof row ) X 5 (sizeof column ) X 2 ( since integer requires 2 bytes)
total bytes = 60
- The following program demonstrates reading four values into array and displaying on the screen.
/* program to demonstrate the use of multi-dimension array. */
#include "stdio.h"
void main(void)
{
int x[2][2][2]; /* this declares integer array of 2 x 2 x 2 */
int i, j, m;
clrscr();
/* read data from the keyboard */
for ( m=0 ; m < 2 ; m++ ) // iterates over matrix
{
for ( i=0 ; i < 2 ; i++ ) // iterates over rows
{
for ( j=0 ; j < 2 ; j++ ) // columns in current row
{
printf(“\n Enter x[%d][%d][%d]:”, m,i,j ) ;
scanf( “ %d “ , &x [m][i][j] ) ;
}
}
}
/* display contents of marks */
for ( m=0 ; m < 2 ; m++ ) // iterates over matrix
{
for ( i=0 ; i < 2 ; i++ ) // iterates over rows
{
for ( j=0 ; j < 2 ; j++ )// iterates over columns in current row
{
printf(“\t %d “, x[m][i][j]) ;
}
printf( “\n” ) ; // prints new row on new line
}
printf( “\n” ) ; // prints new matrix on new line
}
}